ウィルソン素数 (1～10000)
未解決問題 : ウィルソン素数は無限に存在するか？
1282279
- 1 + 20 p
1306817
- 1 - 30 p
1308491
- 1 - 55 p
1433813
- 1 - 32 p
1638347
- 1 - 45 p
1640147
- 1 - 88 p
1647931
- 1 + 14 p
1666403
- 1 + 99 p
1750901
- 1 + 34 p
1851953
- 1 - 50 p
2031053
- 1 - 18 p
2278343
- 1 + 21 p
2313083
- 1 + 15 p
2695933
- 1 - 73 p
3640753
- 1 + 69 p
3677071
- 1 - 32 p
3764437
- 1 - 99 p
3958621
- 1 + 75 p
5062469
- 1 + 39 p
5063803
- 1 + 40 p
6331519
- 1 + 91 p
6706067
- 1 + 45 p
7392257
- 1 + 40 p
8315831
- 1 + 3 p
8871167
- 1 - 85 p
9278443
- 1 - 75 p
9615329
- 1 + 27 p
9756727
- 1 + 23 p
10746881
- 1 - 7 p
11465149
- 1 - 62 p
11512541
- 1 - 26 p
11892977
- 1 - 7 p
12632117
- 1 - 27 p
12893203
- 1 - 53 p
14296621
- 1 + 2 p
16711069
- 1 + 95 p
16738091
- 1 + 58 p
17879887
- 1 + 63 p
19344553
- 1 - 93 p
19365641
- 1 + 75 p
20951477
- 1 + 25 p
20972977
- 1 + 58 p
21561013
- 1 - 90 p
23818681
- 1 + 23 p
27783521
- 1 - 51 p
27812887
- 1 + 21 p
29085907
- 1 + 9 p
29327513
- 1 + 13 p
30959321
- 1 + 24 p
33187157
- 1 + 60 p
33968041
- 1 + 12 p
39198017
- 1 - 7 p
45920923
- 1 - 63 p
51802061
- 1 + 4 p
53188379
- 1 - 54 p
56151923
- 1 - 1 p
57526411
- 1 - 66 p
64197799
- 1 + 13 p
72818227
- 1 - 27 p
87467099
- 1 - 2 p
91926437
- 1 - 32 p
92191909
- 1 + 94 p
93445061
- 1 - 30 p
93559087
- 1 - 3 p
94510219
- 1 - 69 p
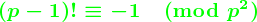
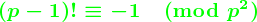
．B = 0 のときウィルソン素数になる．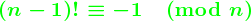
が成り立つ．